Dynamics of information into chaotic systems
This research operation is conducted in IUSTI laboratory of Polytech' Marseille by Philippe Guillemant with the collaboration of Pr Marc Medale and Cherifa Abid. It is trying to demonstrate the feasability of a new approach of non linear dynamical systems (and even space-time itself) that is consisting in the introduction of atemporal parameters (or extra dimensions) so as to describe the multiplicity of possible final states, appearing when the limit of precision make them, when time is growing, more and more independant of initial conditions. Though this work was at the beginning oriented for practical interests, it is not exempt of daring consequences, when we take into account the possibility for at least one of these hypothesis to be true:
These 4 hypothesis are clearly linked and lead us to focus on the concept of information : how is evolving phase information during computations, and in particular the amount of its associated required memory ? At which step is it necessary to stop calculations if we want to maintain a perfect determinism from initial conditions ? Is it possible to quantify the number of different branches which appear after this step ? How much dimensions are necessary to restore determinism in a discrete space-time ?
Considering these questions as essential, we have recently made this publication (in press):
"A discrete classical space-time could require 6 extra-dimensions",
Annals of physics 388 (2018) 428-442
ABSTRACT:
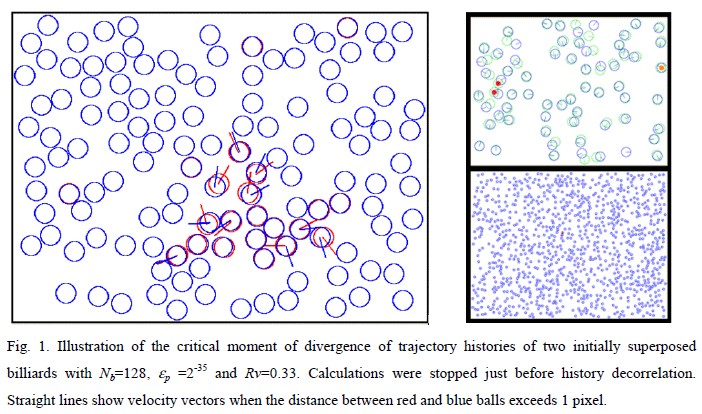
We consider the possibility for our space-time to be discrete and for the laws of the Universe to be implemented in a computational way, in correlation with the principle according to which the density of information is bounded. We use the small-scale model of the 2D billiard to study the consequences of such a boundary on ball phase uncertainties, in calculating their propagation after each shock and estimating the corresponding loss of phase information. Our main result is the measurement of a critical time step above which billiard calculations are no longer deterministic, meaning that a multiverse of distinct billiard histories begins to appear, caused by the lack of information. We then highlight unexpected properties of this time step and the subsequent exponential evolution of the number of histories with time to observe that after a certain duration, all billiard states could become possible final states, independent of initial conditions. We conclude that if our space-time was really a discrete one, we could need to add still unknown atemporal laws of the Universe to our computation, so as to calculate extra-dimensions in order to specify which history should be played.
CONCLUSION:
In a discrete space-time of finite density of information, it turns out from our computations that the amount of deterministic information that is calculable using physical laws is of the same order as the amount of information that is contained into initial conditions. This suggests a possible incompleteness of governing laws at discrete level. Our results then imply that a 3D discrete space-time would need 3 additional dimensions to specify final conditions, and even 6 extra ones if one supposes the existence of alternative present paths, like in many-worlds theory. In particular, we have argued for the possibility for final conditions of a sufficiently distant future of our universe to be at least partially independent of our present state, which seems interesting if only because it would preserve a chance for free will.
Though it is attractive to characterize a unique version of our Universe within the multiverse by postulating the uniqueness of its present state, one can wonder how many extra-dimensions are necessary. Our work suggests a discrete space-time could require up to 6 extra-dimensions. This should be interpreted as highlighting the fact that our known physical laws of the Universe could still be incomplete to describe reality, and that we would need complementary laws. As it should be in the present case timeless ones, we guess that quantum gravity emerging from Wheeler Dewitt equation [22] could bring key elements to compensate the loss of information, so as to calculate extra dimensions and then restore determinism.
***
|
Philippe Guillemant |
Philippe Guillemant is a distinguished research engineer at the French National Centre for Scientific Research (CNRS), making interdisciplinary research that is connecting neurosciences, artificial intelligence and non linear dynamical systems. He is the inventor of a new artificial vision technology that is used into visual systems of humanoid and industrial robots, for which he received numerous awards, including the CNRS Cristal. He is the cofounder of 2 startups marketing this technology and has authored or co-authored 4 international patents, 30 journal papers or conference proceedings, 2 books of scientific popularization and various articles in general public reviews like TimeMatters. |
|
Marc Medale |
Marc Medale (Biographical Sketch) is a professor of mechanical engineering at Aix-Marseille University in France. His research is mainly focused on computational fluid dynamics, especially incompressible or thermal flow instability problems, for which he has obtained reference results and benchmarks. He developed different computational models capable to adress branches of steady state solutions and to detect bifurcation points. He is coordinating an international and collaborative education program with the College of Engineering of the University of Iowa (USA). He has authored and coauthored 48 journal papers, 46 conference proceedings and 3 chapters in collaborative books. |
|
Cherifa Abid |
Cherifa Abid is an associate professor at Polytech' Marseille in France. Her main topics are heat transfer, thermoconvective instabilities and solar energy. She is the author or co-author of 100 papers published in scientific journals and conference proceedings. She is member of various international conferences and expert for many scientific journals. |